Verifiable delay functions on Bitcoin
This post was first published on Medium.
A Verifiable Delay Function (VDF) is a function that takes a significant amount sequential calculation to evaluate, but is quick to verify. We have implemented it on Bitcoin for the first time. VDF, as a cryptographic primitive, can be used to build a multitude of new applications, such as public random beacons, computational timestamping, and proof of data replication.
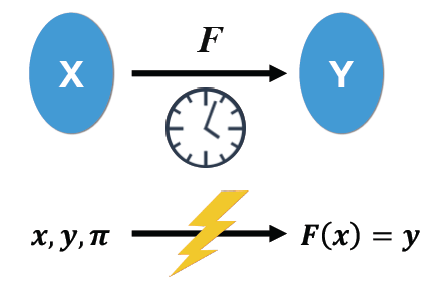
VDF
Motivations
Random beacon on chain
Achieving randomness is difficult in a blockchain since everything is deterministic and public. A classic example is a smart betting contract between two parties, where one party wins if the next block hash is even, and the other wins if it is odd. A miner can cheat this contract by playing it while ignoring any new block that causes him to lose his stake.
A VDF alleviates this problem by requiring the randomness to come not from the block itself, but from a VDF of it. By setting the VDF to take a long time to calculate, say one hour, a miner is discouraged from cheating by losing mining rewards in found blocks for the next hour, since it is greater than the stake amount.
Lottery
In a similar example, Alice, Bob, and Charlie would like to play a lottery round, which requires them to jointly generate a random number to determine the winner. In a naive approach, each of them publishes a random number. Once all participants have done so, they calculate a hash of the sum of the published numbers.
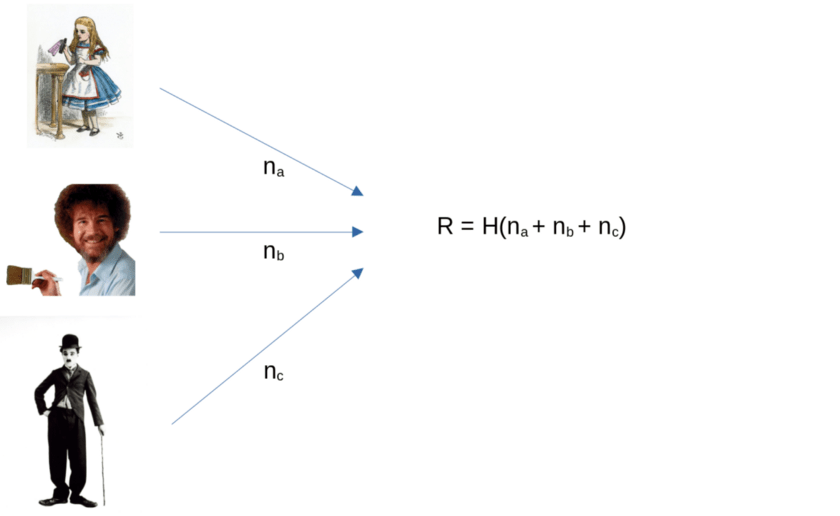
The problem is that the last person to submit their number can control the outcome. For example, if Alice and Bob have already submitted their values, Charlie can just try calculating the result using different numbers until he finds a number that gives the result he wants.
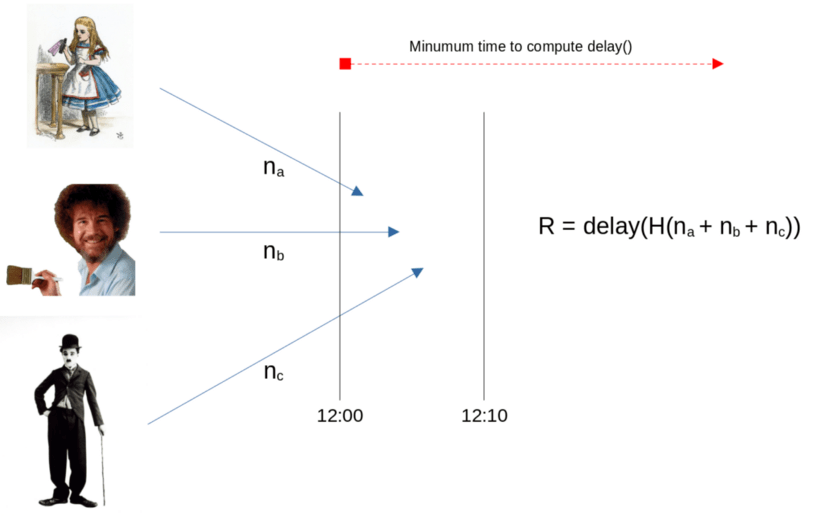
To overcome this problem, we introduce a delay using VDF. Let’s say contestants have to submit their numbers between 12.00 and 12.10. After all the numbers are submitted (or timed out), they are hashed again, and a VDF is evaluated on the resulting hash that takes longer to evaluate than 10 minutes, such as an hour. Now Charlie could not cheat as the time to evaluate the result is longer than the submission window.
Formal definitions
A valid VDF f must have the following properties:
- Sequential: everyone can calculate f(x) in sequential steps. Note that it is important that the calculation cannot be parallelised. This ensures that an attacker cannot simply speed up the computation by using more resources. Computation time is limited solely by the speed of a single execution thread.
- Effectively verifiable: given the output yany observer can confirm that y = f(x) in a short time, to be precise log
VDFs are a way to provably slow things down. They introduce a forced time delay to an output so that malicious actors cannot influence it by predicting future values.
VDF vs proof of work
VDFs and Proof of Work (PoW) are both difficult to calculate but easy to verify. The fundamental difference is that PoW can be parallelized, while VDFs cannot.
Implementation
Since a VDF is effectively verifiable, we can verify it in a smart contract. We have implemented a verifier for a popular VDF developed by Wesolowski.
VDF can be represented as the following function:

x is the input value, T is the delay parameter publicly known and determines the duration of the delay, and y is the output.
To calculate x^ 2 ^ Tmust we calculate sequentially x^ 2 ^ i with I from 0 to T. It is crucial that the repeated squaring calculation is not parallelizable.
To make it effectively verifiable, so that a verifier doesn’t have to follow it all T step again, the following interactive protocol is run. The protocol can be made non-interactive using the Fiat–Shamir heuristic.

The verifier is implemented below.
The full code, along with tests, can be found on GitHub.
See: The presentation of the BSV Global Blockchain Convention, Smart Contracts and Computation on BSV
width=”562″ height=”315″ frameborder=”0″ allowfullscreen=”allowfullscreen”>
New to Bitcoin? Check out CoinGeeks Bitcoin for beginners section, the ultimate resource guide for learning more about Bitcoin – as originally envisioned by Satoshi Nakamoto – and blockchain.


