Scalable Peer-to-Peer Tokens on Bitcoin: Solve the Back-to-Genesis Problem Using Recursive SNARKs

This post was first published on Medium.

This is an implementation of nChain’s solution¹.

Back to the Genesis problem

Bitcoin tokens are usually stored in UTXOs. When a supposed token transaction is received, a user needs a way to efficiently and quickly check its authenticity. A big part is determining whether it connects to a specific originating transaction, where the token is issued.

In a basic form, the Back-to-Genesis (B2G) problem boils down to: given a transaction, is it linked to a particular originating transaction in an unbroken chain of transactions?

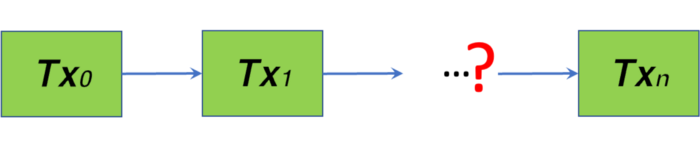
All tokens on Bitcoin today must rely on a trusted third party to solve the problem, as it becomes computationally challenging for a lightweight user to verify themselves when the chain is too long². For example, DotWallet’s Badge tokens use a token indexer and Sensible tokens use an oracle. This third-party dependency hinders token adoption on Bitcoin, as it is not as scalable and SPV-friendly as native bitcoins.

Our previous proposal tries to solve the problem without any third party. However, the size of a token transaction grows exponentially as the chain grows, which severely limits its use in practice.

Recursive SNARKs

Recall in a recursive SNARK, specifically incrementally verifiable computation (IVC), we wish to prove that a function F applied n times to initial input z₀ yields zₙ.

In each step, zᵢ is the public input and wᵢ the private input (i.e. witness).

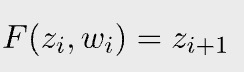
Each step produces a new proof. In step Icomputes the proof algorithm 𝛑ᵢ that proves all steps up to I are correct, using only local information from the last step and the current step as shown below. Crucially, it does not backtrack to step 0, while still being able to verify all steps since step 0 is correctly performed.

Prover algorithm: compute proof step by step

Using recursive SNARKs on B2G

IVC naturally leads to an elegant solution to the B2G problem.

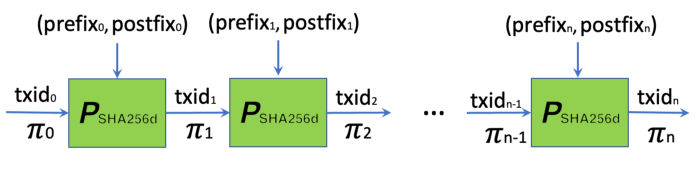
IVC in B2G

Specifically, the IVC is instantiated as follows:

• zᵢ: txidᵢ, the transaction ID of the ith transaction in the chain
• wᵢ: the remainder of the i-th transaction. We divide it into two parts: prefixᵢ and postfixᵢ, which represent what comes before and after txidᵢ.
• function F: the txide of a transaction is the double SHA256 of it and (i+1)-th the transaction uses i-th the transaction, its txid and thus F is calculated as below:

txid is the red box part, prefix/postfix is everything before/after that respectively. || is interconnection.

A transaction

We can now prove a transaction descending from a given transaction by verifying a single short proof regardless of the length of the transaction chain, without tracing all the way back.

A simple NFT token protocol

Let’s construct a simple NFT token using the above method. An NFT is characterized in an issuing transaction, also known as an origination transaction. For simplicity, let’s just use one input and one output in each transfer transaction³.

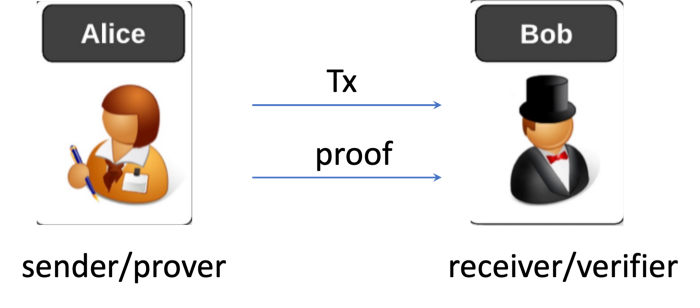
When Alice transfers an NFT to Bob, she constructs a transaction with Bob as the recipient and gives it to Bob directly off-chain. Thanks to the peer-to-peer nature of Bitcoin, she also sends a SNARK proof along with the transaction. Alice can generate the proof without tracing to the genesis transaction that we explained earlier.

Bob only accepts the NFT if both checks pass:

1. he validates the transaction using SPV, similar to a regular bitcoin payment
2. he confirms the proof⁴.

Without the first check, an attacker can create alternative transaction chain originating from the originating transaction, but is not on the Bitcoin blockchain. Without the second check, the token transaction may not connect to the genesis transaction.

The proof is of constant size of only a few KB and can be verified in seconds regardless of the chain length, with negligible overhead. The token transfer is actually instant, just like a normal bitcoin payment.

Proof time

The most time-consuming part of recursive SNARKs is generating a proof, which can be up to a minute on a resource-constrained device. To enable instant token transfer, a proof can be precomputed as soon as a token is received by Bob, so that it is ready when Bob transfers it to the next owner. In the case where Bob needs to send the token to Charlie immediately after receiving it from Alice, he can send the old proof received from Alice and have Charlie verify the last two links in the transaction chain, without generating a new proof as a backup .

Implementation

We have implemented the recursive SNARK using snarkyjs as below.

Recursive B2G proof

To start, we must first compile the program to get the verification key. Note that it is no reliable setup.

The key can be made public in a central registry associated with the originating transaction, or it can be placed in another output of the originating transaction.

The genesis method starting from line 5 is called to generate the first proof, which only checks txid0 is the genesis transaction ID on line 9.

The transfer method starting from line 13 is called to generate a new proof attesting to:

• last proof is valid on line 17
• the current transaction uses the last transaction on lines 18 and 19.

Finally, we can verify a proof against the verification key.

The full code can be found in this Github repo.

Summary

We present only a simple NFT example using recursive SNARKs. It can be extended to a directed acyclic graph (DAG), rather than a chain of transactions. It can also be extended to include fungible tokens or other use cases where a user must effectively ensure that a transaction can be linked to an ancestor transaction.

Recognitions

We thank nChain for sharing the original idea of ​​applying recursive SNARKs to the B2G problem. We also thank Gregor Mitscha-Baude of O(1) Labs for his help with the implementation of the SHA256 circuit.

***

NOTES:

[1] WP1590 Transaction Chain Proof, MS Kiraz and O. Vaughan, patent application GB2200400.6.

[2] In a more general form, transactions form a directed acyclic graph (DAG), which makes the solution of B2G even more computationally intensive.

[3] This can be enforced in a smart contract or the SNARK circuit, or both. In the former, we can use the OP_PUSH_TX technique to limit the number of inputs and outputs in all transactions descending from the genesis transaction. For example, we can enforce that any NFT transaction has two inputs and one output. The second entry covers transaction fees.

[4] Optionally, the proof verification can be done on a chain. It only requires implementing the verifier in the snarkyjs proof system, similar to the Groth16 verifier we have implemented.

See: The presentation of the BSV Global Blockchain Convention, Smart Contracts and Computation on BSV

New to Bitcoin? Check out CoinGeeks Bitcoin for beginners section, the ultimate resource guide for learning more about Bitcoin – originally envisioned by Satoshi Nakamoto – and blockchain.