Effective zk-SNARKs on Bitcoin: Technical Explanation
This post was first published on Medium.
Implement Groth16 in sCrypt
Recently we implemented zk-SNARKs in sCrypt and ran it on Bitcoin. More specifically, we have implemented the verifier of the Groth16 algorithm, which allows a zero-knowledge proof to be verified directly on-chain. This article dives into some of the details, shedding light on how to effectively implement other advanced cryptographic techniques on Bitcoin.
Bilinear pairings on elliptic curves
Groth16 has extremely small sample size and fast verification. Pairing is the most expensive part of the Groth16 verifier algorithm. We have chosen the optimal Ate pairing, since its effectiveness has been demonstrated in practice.
We implement it over the mating elliptic curve BN256 (also known as ALT_BN128 and BN254). We use BN256 since it is 1) supported by popular ZKP tools like ZoKrates and Circom; 2) compatible with other blockchains like Ethereum.
Miller’s algorithm is used to efficiently calculate the optimal Ate pairing. At a high level, it consists of two parts:
- Miller loop: calculate an intermediate function of the two input points f(P, Q) recursively
- Final exponentiation: raising f to a great power c
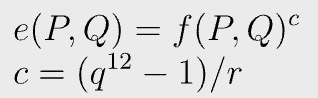

Reduce to 3 pairings
The verifier must check whether the following equation holds.

We have 4 pairings in total. We notice that a and β is known by setup, so we precalculate the other pairing and add it as part of the verification key, saving a pairing.
One last exponentiation
Eq. 1 can be rewritten as:
![]()
It can again be written as the following, since e is bilinear and we can shift the exponent (-1) into the bracket.
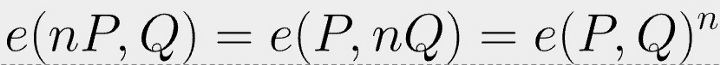
![]()
Plugging in Eq. 2, we get:
![]()
Instead of calculating finite exponentiation 4 times, which are computationally intensive, we just need to do that once finally.
Loop rollout
In sCrypt/Script, everyone if branches are included in a transaction and incur transaction fees, regardless of whether they are executed later or not. In the mill loop, sᵢ is known at compile time. We roll out the loop and avoid branching on lines 5 and 7.
Extension field twist
Computational pairing of two points requires direct elliptic curve arithmetic over extension fields Fq¹², which is extremely complicated and inefficient. We use a twist to map it Fq², which drastically improves efficiency. See this article for more detailed explanation.
Summary
After all these optimizations we are able to cut the script size for linking with 100X to 5MB. We are exploring several optimizations to further reduce it. The full version of the code can be found on GitHub.
Traditionally, the goal of optimizing a program is to minimize CPU and/or memory usage. In Bitcoin where the transaction fee is proportional to the size of a transaction containing the script, the goal is to minimize the script size. How to optimize towards this goal is an interesting open topic worthy of new research.
See: The presentation of the BSV Global Blockchain Convention, Smart Contracts and Computation on BSV
width=”560″ height=”315″ frameborder=”0″ allowfullscreen=”allowfullscreen”>
New to Bitcoin? Check out CoinGeeks Bitcoin for beginners section, the ultimate resource guide for learning more about Bitcoin – originally envisioned by Satoshi Nakamoto – and blockchain.

